1.从代价函数谈起SVM
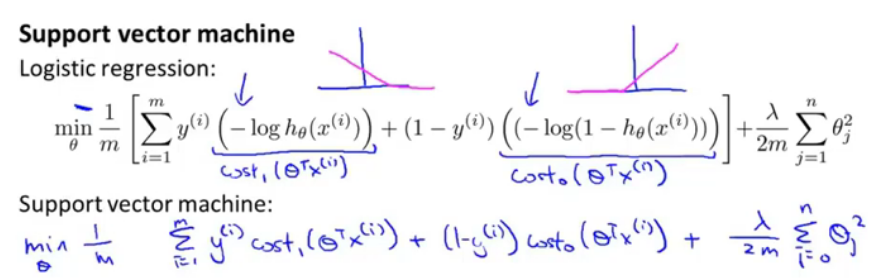
图一
根据将y=0||y=1,得到逻辑回归的代价函数,那么SVM和其代价函数是相似的,只不过是引入了cost0与cost1,并且自变量使用了theta_T*x(i),并且由于SVM的通常表示方法,得到了如下的优化函数假设:

在代价函数项加上了系数C(=1/lamda),也就是C很小时,后边一项的权重较大,SVM的模型,如果theta_T*x>=0,那么模型输出1,否则输出0.
SVM就是将负样本和正样本以最大间距分开。

优化目标如上,当要最小化时,C若设置为非常大时,那么要让第一项为0,当一个样本是yi=1时,就需要θTxi>=1,这个是跟据类斯ReLU函数来决定的;
当一个样本是yi=0时,那么第一项中只有后半部分在,就要求θTxi<=-1这一项就为0了;
那么当第一项为0之后,就是最小化第二项的问题了。min后一项,并且限制条件是右下角(只有满足条件才可以保证前一项为0啊!)
2.SVM为何能选取最大间隔的平面?
图二
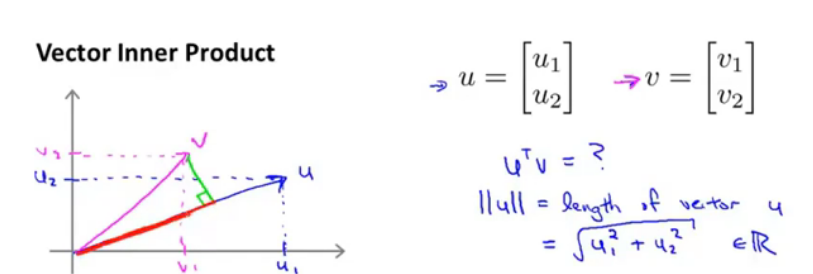
向量的内积,对单个向量来说,它的第二范数也就相当于是向量的长度(从原点出发),而内积相当于v在u上的投影长度(有正有负)*u的长度。
图三
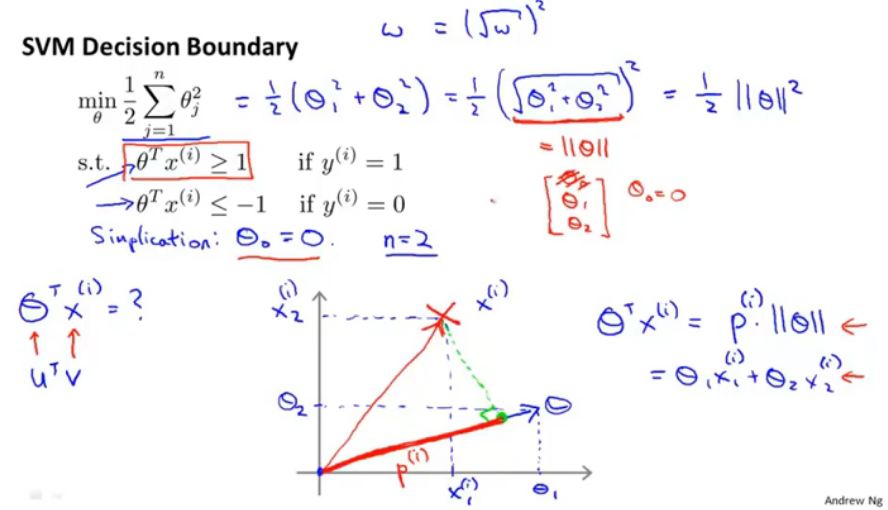
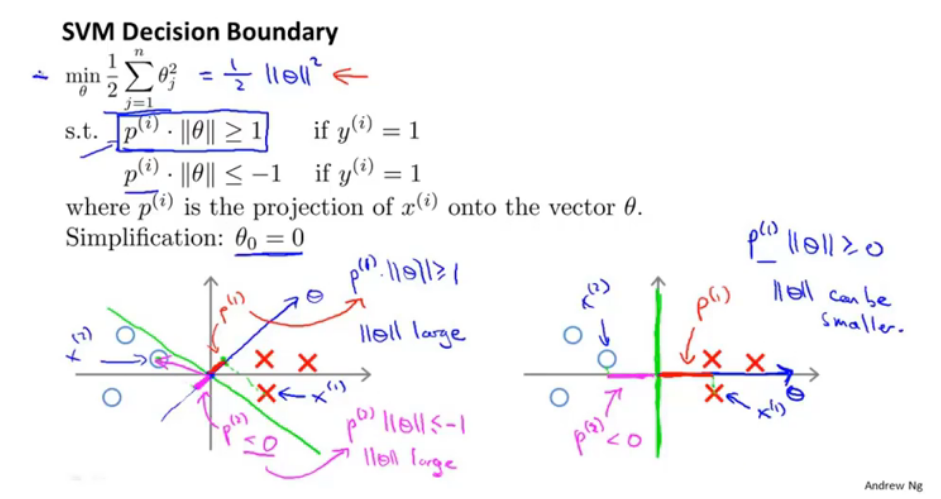
当只有两个特征时,theta1和theta2即相当于theta向量的范数的平方,而通过公式(右下角)将优化条件限制为正样本点在分割平面的正侧法线(theta向量方向)的投影长度*theta向量的长度,所以就min||theta||的同时需要保证条件≥1,就需要正样本点在theta方向上的投影值最大。如下图:
图四
//PS不太明白,为什么theta向量是和超平面垂直的?保留问题。
3.高斯核函数原理介绍

图五
给出三个标志点,对任一数据点x,都计算,计算x和三个给定点的相似度,计算相似度的公式图中给出的是高斯核函数,即x与每个点的距离的平方/-2*6^2,这个相似度函数就是核函数。又给出了一个十分传神的例子:
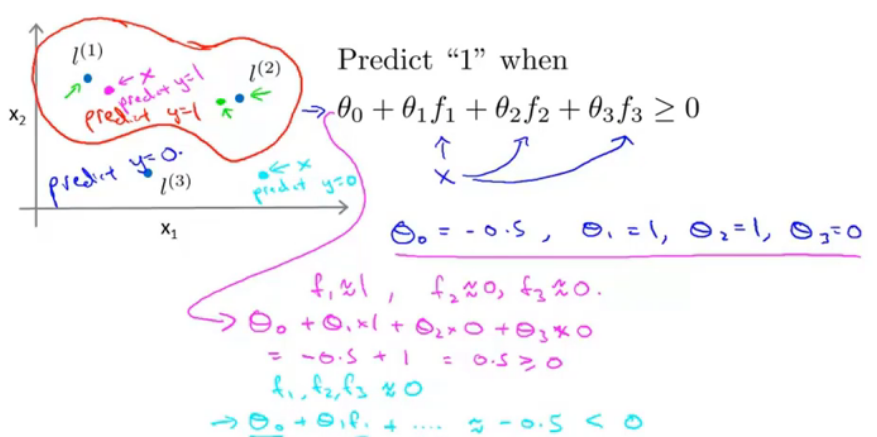
图六
当?≥0时,预测类为正类,那么取theta为以下,根据高斯和函数的性质,如果点x和l距离很近,那么≈1;距离很远,那么结果≈0。通过这样就可以得出一个分界面。这是一个我从前没有了解过的角度!下一节就讲到该如何选取这些landmark。
4.高斯核函数中landmark的选取

图七
这里的landmark选取是通过将训练集中的每个点都作为landmark,共m个,给定一个点,那么就会计算与其他所有点的相似度,其中会有一个是与自身的相似度,那么就=1,这样通过相似度函数,也就是核函数,可以将原本的x(i)映射到一个m+1维的f向量中,并且让f去参与运算,f就是用于描述训练样本的特征向量。

图八
在8中,使用f去计算,并且损失函数中代入f去计算,所以最终优化项中求和是从1求到m,或者说n=m.//不太明白这里相等是什么意思。通常theta^2求和都被写为thetaTtheta. 还有中间加上M的,不太明白是什么意思。
大多数SVM实现的时候,是将thetaTtheta替换为中间*M(M取决于使用的核函数),这是另一种区别于求||theta||^2的距离求解方式。这种方式让SVM运行更加高效,适用于有更大的训练集。主要是为了运算效率。
5.SVM参数中偏差-方差的问题

图九
C也就相当于逻辑回归正则化项系数的倒数,当C很大时,即lamd较小,也就是忽略正则化项,偏差较小,方差较大,(是说系数向量吗?);当C很小时,即lamd较大,即计算正则化项,那么偏差较大(即欠拟合状态)方差较小。而对应高斯核函数中的参数6^2,当其较大时,函数趋于平滑,偏差较大,方差较小;当其较小时,偏差较小,方差较大。//不太明白是什么意思。
6.SVM中的核函数适用情况

图十
使用SVM软件包来找出参数theta,需要指明参数C和使用的核函数:
没有核函数(即线性核函数):适用于当n很大,m很小,即特征很多,但是样本量少的情况。
高斯核函数:还需要指明参数6^2,当n较小,m很大时,即特征较少,样本量大的情况。这两个核函数是最常见的,也是使用最频繁的。
在使用核函数时还需要注意的问题,就是归一化,如下图:

图十一
在使用核函数计算特征向量时,需要对输入向量进行归一化,如当一个特征是房价,另一个是卧室数量,那么v的大小就只受房价控制了。
7.其他的核函数

图十二
多项式核函数,有12中的几种形式,使用它时需要指明常数与幂次。还有更多的,字符串核函数(在做文本分类时,需要计算不同的字符串之间的距离)
8.使用逻辑回归orSVM

图十三
1.当特征数较大时(n>=m,n=10,000,m=10-1000),这时候使用逻辑回归或者没有核函数的SVM,(因为若使用复杂的核函数训练复杂的分类函数,可能会出现过拟合的情况)
2.当n较小时,m是中等的(n=1-1000,m=10-10,000),此时使用高斯核函数的SVM最优。
3.当n较小,m较大时,增加更多的特征,然后使用逻辑回归和没有核函数的SVM。
神经网络能够很好的解决所有的问题,但是训练时间会稍长一点。